前回の続き=選択問題の2個目の小問です。この問題を解いている状況と時間帯によって、時間を使って解きに行くか、残した別の問題に戻るか など柔軟な対応が必要です。今回の場合は、小問(b)もとっつき悪い割には、簡単に解けるので残り時間と相談しながら解きたいところです。
令和4年度下期 第三種電気主任技術者試験 理論科目 問17(b)

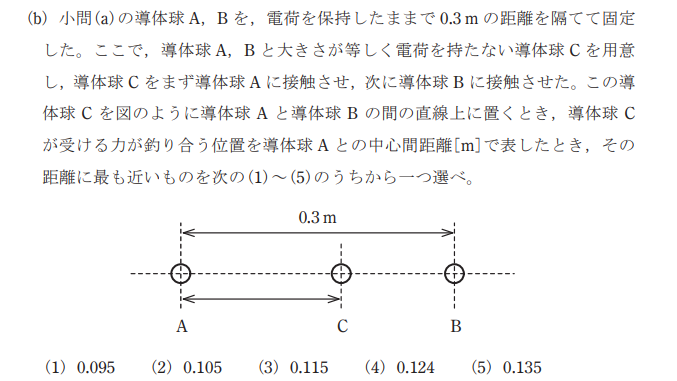
出典:令和4年度下期 第三種電気主任技術者試験 理論科目 問題 問17(b)
導体球を接触させる というのが混乱させますが、要は接触したら同じ電荷を持つ と分かれば解けます。もちろん、2個の導体球の合計の電荷は同じままという前提です。
まず、導体球AとCが接することで電荷は2つに等しく分けられます。もともと導体球Aに2*10−8の電荷があったとすると、AとCはそれぞれ1*10−8の電荷になります。
その後、導体球BとCが接する場合、Bが3*10−8,Cが1*10−8の電荷を持つので、B、C合計で4*10−8が等分されるので2*10−8ずつになります。
問題文に2つの電荷に働く力は、電荷の積に比例し距離の二乗に反比例する とあるので、導体球A-C間、B-C間の力が釣り合う距離をa、bとすると
1*10−8*2*10−8/a2 =(2*10−8)2/b2 ・・・(1)
a+b=0.3 ・・・(2)
(1)より b2=2a2 ・・・(3)
(2)より b=0.3ーa ・・・(4)
(4)を(3)に代入して
(0.3ーa)2=2a2
(0.09ー0.6a+a2)=2a2
0=a2+0.6aー0.09
a={−0.6+0.6√2}/2
=0.3(√2−1)≒0.1242
選択肢は(4)
導体球の接触を解釈できれば、意外と簡単です。取りたいところの問題ですね。以上何か参考になったら嬉しいです。